前回、売上実績サンプルデータについて重回帰分析を用いて売上予測を行いましたが結果はいまいちでした。
今回は自分で作るのではなく、季節性を考慮した時系列解析の手法である、SARIMAを用いて将来の売上予測をしてみたいと思います。
季節自己回帰和分移動平均の準備
まずは、いつも同様、Google Colaboratoryへアクセスし、Google DriveのマウントとMatplotlibの日本語表示のためのフォントインストールおよびキャッシュの削除、売上実績サンプルエクセルデータのDataframeへの読み込みまでを済ませておきます。
from google.colab import drive
drive.mount(‘/content/drive’)
!apt-get -y install fonts-ipafont-gothic
!rm /root/.cache/matplotlib/fontlist-v310.json
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import matplotlib
%matplotlib inline
filepath=”/content/drive/My Drive/Colab Notebooks/売上実績sample.xlsx”
df_a = pd.read_excel(filepath,usecols=[0,1,2])
df_a[‘年月’]=df_a[‘年’].astype(str) + ‘/’ + df_a[‘月’].astype(str)
df_a = df_a.loc[:,[‘年月’,’売上高’]]
SARIMA(季節自己回帰和分移動平均)とは?
SARIMA自体の手法についても、文献やネット上にいっぱい情報があるため、ここでも利用にフォーカスし、詳細な内容は割愛したいと思いますが、概念としては、こちらがわかりやすかったため、こちらを参考にさせていただきました。周期データをAR(自己回帰モデル)とMR(移動平均モデル)を組み合わせて定式化したARMRモデルに、トレンドと季節周期性を加味したもののようです。売上実績サンプルデータは単純な周期ではなく、下降?トレンドもありそうなので、ちょっと期待できそうです。
必要なライブラリのインポート
必要なライブラリをインポートしておきます。回帰分析はscikit-learnライブラリを利用したので、今回はstatsmodelsライブラリを使用してみます。
import statsmodels.api as sm
予測モデル作成までの事前処理
前回同様、df_a.iloc[:,1]は、df_aデータフレームの全ての行(:)、1列目(実際には0から始まるので2列目)を意味しています。raw_dataには売上実績データ自体がすべて入るイメージです。
今回も、日付を相対的に扱いたいので、dateutil.realativedeltaライブラリのrelativedeltaクラスをインポートします。今回も日付は後で相対的に足し算、引き算できるようにdatetime型に変換してu_dateymに格納しています。
その後、future_dateリストに将来の日付を入れて、最後にu_dateymに結合しています。
この処理で、実績データの最初の月から売上予測の最後の月の日付がu_dateymに入りました。
#何個の連続データを対象にするか
length = 12
# Future用のデータ数
future_d = 12
# Further Future用のデータ数
f_future_d = 70
from dateutil.relativedelta import relativedelta
filepath=”/content/drive/My Drive/Colab Notebooks/売上実績sample.xlsx”
df_a = pd.read_excel(filepath,usecols=[0,1,2],parse_dates=[[‘年’, ‘月’]])
u_dateym = pd.to_datetime(df_a.iloc[:,0])
#リスト作成
further_date = []
dm_num=len(df_a[‘年_月’])
dm_last=u_dateym.iloc[dm_num-1]
for i in range(1,f_future_d + 1):
further_date.append(dm_last + relativedelta(months=i))
#日付結合u_dateym = pd.concat([u_dateym,pd.Series(data = further_date)],axis=0)
この後、データに複数視点で確認してみます。
(確認1)元データを分解してみる
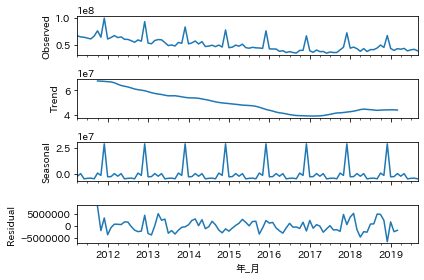
トレンド、季節周期に分解して確認してみます。グラフのObservedは元データです。周期性があり、特にトレンドは落ち続けた後に少し戻している感じになっています。Residualは残差です。残差はゼロに近いほどフィットしていますが、残差が大きくなっているところもちらほら見受けられます。
df_a = df_a.set_index([‘年_月’])
res = sm.tsa.seasonal_decompose(df_a, freq=length)
fig = res.plot();
(確認2)標本自己相関(ACF)と標本偏自己相関(PACF)
fig, axes = plt.subplots(1, 2)
#標本自己相関(ACF)
sm.tsa.graphics.plot_acf(df_a, ax=axes[0]);
#標本偏自己相関(PACF)
sm.tsa.graphics.plot_pacf(df_a, ax=axes[1]);
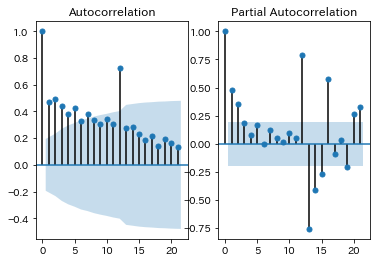
周期性があるかどうか、自己相関係数で確認してみます。グラフの薄い青エリアは95%信頼区間で、そのエリア外のところは、有意に関係があると言えるかと思います。ACFの方は、元データと、1月ずつずらした(ラグ)データとの相関係数なので、12ずらしたところが高くなっていることから、12ヶ月の周期性はあるのかな?と思われます。24が表示されていないので微妙ですが。。ACFはコレログラムとも言うようです。標本偏自己相関(PACF)は2点間の相関係数のようなのですが、これからも12ずらしたところが正の相関関係があり、13のところは負の相関関係があるように見えます。
(確認3)階差と季節性除去
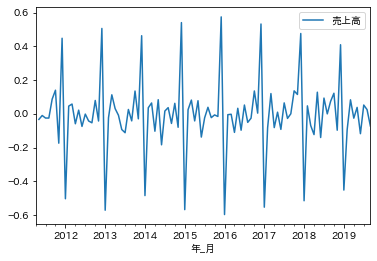
前後の差分データ(階差)を用いて、時系列データ間の規則性を確認してみます。データは見やすいように対数変換しています。対数化はデータのばらつきを-1から1に合わせて変数間のデータの大きさの影響をなくす効果もありますが、今回は売上データ一つなのその点の効果はなさそうです。季節性を除去したときの規則性も確認してみます。差分データからも周期性は確認できそうです。
ldf = np.log(df_a)
ldf.diff().plot()
(確認4)単位根検定で単位根がないと言えるかを確認認
ytが非定常過程、また差分系列yt−yt−1=Δytが定常過程である時、ytは単位根過程であると言うそうです。単位根過程であるということは、ytには何の規則性もないのに、たまたま回帰っぽくなっている「見せかけの回帰」ということでしょうか。単位根検定の一つであるADF検定の帰無仮説は”単位根がある”、
対立仮説は”単位根がない”です。 ADF検定でp値が0.05以下であれば、帰無仮説は棄却でき、単位根はないと言えそうです。単位根はまったくランダムで相関のない累積和ですので、単位根はないといえるということは、時系列データは自己相関があると言えそうです。
sm.tsa.adfuller(df_a[‘売上高’])[1]
出力は0.132891175414655で、p値は0.05より大きくなりました。ですので、単位根はないとは言い切れないということになります。ただ、これは単位根があるということの証明ではないため、ひとまず進めてみます。
モデルの作成
SARIMAで指定する、ARIMAの次元(order)と季節変動の次元(seasonal_order)はいくつか試して情報量基準 (AIC)が最小になるものを選びました。AICは赤池の情報量基準で小さければ小さいほど良いモデルとなるようです。
mod_seasonal = sm.tsa.SARIMAX(ldf, trend=’c’, order=(1, 1, 1),seasonal_order=(1,0,1,length))
res_seasonal = mod_seasonal.fit()
いよいよグラフ化
下のコードで、前回同様グラフ化してみます。
plt.xticks(np.arange(0, len(u_dateym) + 1, 12),rotation=70)
plt.title(“売上サンプル”, fontsize = 16)
plt.xlabel(‘年月’) plt.ylabel(‘売上高(億円)’)
plt.plot(u_dateym.iloc[0:dm_num].dt.strftime(‘%Y/%m’), df_a[‘売上高’], color=”b”, label=’売上実績’) plt.plot(pd.Series(data=further_date).dt.strftime(‘%Y/%m’), pred.map(lambda x: math.exp(x)), color=”y”, label=”予測”)
plt.legend()
plt.savefig(“predict-sarima.png”,dpi=200, bbox_inches=”tight”, pad_inches=0.1)
plt.show()
plt.close()
出力結果はこちらです。
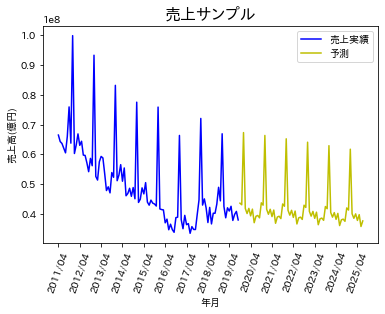
トレンドの予測はある程度できていそうですが、実績データは毎年の売上ピークにでっこみ引っ込みがありますが、予測は一律下降トレンドになっています。この点は、パラメーターを変更すれば改善するのかもしれません。次回はランダムフォレストを用いて予測してみたいと思います。
データマーケティングはプロにお任せください
当社ではデータマーケティングやそのツールの活用に長けたコンサルタントがおります。もし利活用にお困りのことがあればぜひ、お問い合わせください。
さらに、はじまりビジネスパートナーズの推奨する、全国の食品スーパーID-POS高速分析ツール「Real Shopper SM」をIT導入補助金を活用して、賢く導入してみませんか?IT導入補助金に関する特設サイトは以下をクリックしてください。




