前回、売上実績サンプルデータのグラフ化を行いました。
今回は、単回帰分析を用いて将来の売上予測をしてみたいと思います。
データのDataframeへの読み込み
まずは、前回同様、Google Colaboratoryへアクセスし、Google DriveのマウントとMatplotlibの日本語表示のためのフォントインストールおよびキャッシュの削除、売上実績サンプルエクセルデータのDataframeへの読み込みまでを済ませておきます。
from google.colab import drive
drive.mount(‘/content/drive’)
!apt-get -y install fonts-ipafont-gothic
!rm /root/.cache/matplotlib/fontlist-v310.json
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
import matplotlib
%matplotlib inline
filepath=”/content/drive/My Drive/Colab Notebooks/売上実績sample.xlsx”
df_a = pd.read_excel(filepath,usecols=[0,1,2])
df_a[‘年月’]=df_a[‘年’].astype(str) + ‘/’ + df_a[‘月’].astype(str)
df_a = df_a.loc[:,[‘年月’,’売上高’]]
単回帰分析とは?
単回帰分析自体の手法については、文献やネット上にいっぱい情報があるため、ここでは利用にフォーカスし、詳細な内容は割愛したいと思いますが、簡単には各データと二乗誤差が最小となるy=ax+bを見つける形になります。最小なので、aとbそれぞれの偏微分が0となるa(傾き)とb(切片)を求めればよさそうです。
必要なライブラリのインポート
単回帰分析くらいであれば、1から式を作ってでもできそうですが、今回はscikit-learnという、Pythonのオープンソース機械学習ライブラリを利用してみたいと思います。他にstatsmodelsを利用しているケースもありましたが、目的はあくまで売上予測なので、手段は特にこだわらないことにします。Scikit-leamライブラリから最小二乗法のlinear_modelクラスをインポートして、インスタンスを(下ではclf)作っておきます。
from sklearn import linear_model
clf = linear_model.LinearRegression()
予測モデル作成までの事前処理
df_a.iloc[:,1]は、df_aデータフレームの全ての行(:)、1列目(実際には0から始まるので2列目)を意味しています。raw_dataには売上実績データ自体がすべて入るイメージです。
今回は、日付を相対的に扱いたいので、dateutil.realativedeltaライブラリのrelativedeltaクラスをインポートします。X軸データは0,1,2,・・・にするように変換して変数Xに格納しています。Y軸データ(売上実績データ)は変数raw_dataに格納しています。日付は後で相対的に足し算、引き算できるようにdatetime型に変換してu_dateymに格納しています。
from dateutil.relativedelta import relativedelta
raw_data = df_a.iloc[:,1].astype(‘float32’)
u_dateym = pd.to_datetime(df_a.iloc[:,0])
X=pd.DataFrame(list(range(0,len(raw_data))),columns=[‘ID’])
予測結果を入れる空箱(リスト型変数further_date)を作っておきます。日付を計算するためにちょっと小細工しています。試行錯誤しているので、あまりよいやり方ではないかもしれません。。f_future_dには予測する月数(下では70ヶ月)を指定します。これで、実績データ開始月から予測用のすべてがfurther_dateリストに入りました。
f_future_d = 70
further_date = []
dm_num=len(df_a[‘年月’])
dm_last=u_dateym.iloc[dm_num-1]
for i in range(1,f_future_d + 1):
further_date.append(dm_last + relativedelta(months=i))
#日付結合
u_dateym = pd.concat([u_dateym,pd.Series(data = further_date)],axis=0)
モデルの作成
resultにモデルの結果が入ります。空のリストfutureを用意して、予測の70ヶ月分の売上データを入れます。clf.coef_にはモデルの傾き、clf.intercept_にはモデルの切片が入っています。
result = clf.fit(X, raw_data)
future = []
for i in range(len(raw_data) + 1, len(raw_data)+ f_future_d + 1):
future = np.append(future, clf.coef_ * i + clf.intercept_)
clf.coef_を見てみるとarray([-286102.48740465])、clf.interceptは64527126.594327055になっていました。傾きはarrayになっているので、重回帰でもそのまま使えそうです。決定係数clf.score(X,raw_data)は0.4199380391267902で、1に近いほど精度がよいので、あまり精度は良くなさそうです。
いよいよグラフ化
下のコードで、前回同様グラフ化してみます。
plt.rcParams[‘font.family’] = ‘IPAPGothic’
plt.xticks(np.arange(0, len(u_dateym) + 1, 12),rotation=70)
plt.title(“売上サンプル”, fontsize = 16)
plt.xlabel(‘年月’)
plt.ylabel(‘売上高(億円)’)
plt.plot(u_dateym.iloc[0:dm_num].dt.strftime(‘%Y/%m’), df_a[‘売上高’], color=”b”, label=’売上実績’)
plt.plot(range(0, len(raw_data)), clf.predict(X), color=”r”, label=”分析結果”)
plt.plot(pd.Series(data=further_date).dt.strftime(‘%Y/%m’), future, color=”y”, label=”予測”)
plt.legend()
plt.savefig(“predict-senkei.png”,dpi=200, bbox_inches=”tight”, pad_inches=0.1)
plt.show()
plt.close()
出力結果はこちらです。
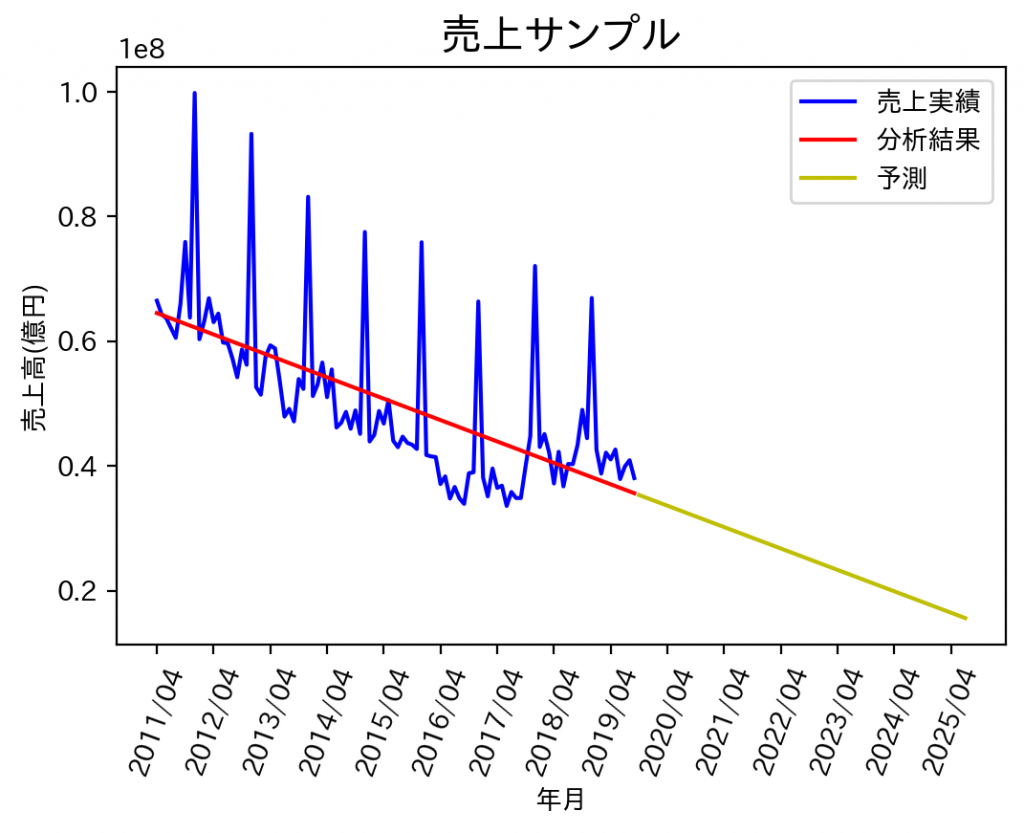
scikit-learnでは、結果はあまり出してくれなさそうです。EXCELで同じデータを回帰分析すると以下のように表示されました。当然ですが切片と傾き、決定係数はscikit-learnの結果と同じです。分散分析はF値がすごく小さく、全部誤差ですっていう帰無仮説は棄却されているので、一応y=ax+bには意味があると言うことかと思います。切片と傾きのp値もすごく小さいので、aもbも有意に0ではないと言えるかと思います。
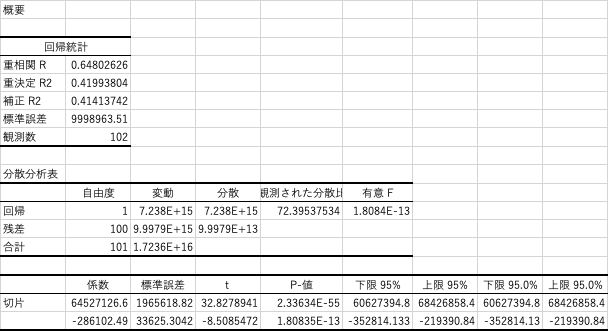
どちらにしても、今までの売上実績の傾向を掴むのには使えそうですが、それを用いて今後の売上を予測していますって言うのは見た目的にも、値的にもちょっと無理がありそうです。売上実績サンプルデータには季節性があるので、その部分をもう一つ説明変数として加えて次回は重回帰分析で売上予測をしてみたいと思います。
データマーケティングはプロにお任せください
当社ではデータマーケティングやそのツールの活用に長けたコンサルタントがおります。もし利活用にお困りのことがあればぜひ、お問い合わせください。
さらに、はじまりビジネスパートナーズの推奨する、全国の食品スーパーID-POS高速分析ツール「Real Shopper SM」をIT導入補助金を活用して、賢く導入してみませんか?IT導入補助金に関する特設サイトは以下をクリックしてください。




